MUSIC
I began this writing in January of 2009 after studying the nature of music for many years and I've continued to refine it up until the present time. The ideas of this writing are scientific, psychological, and philosophical in nature. In order to illustrate the more technical concepts, I've included some mathematics and theory. However, I realize that people have different levels of experience and interest in the technicalities. I hope interested readers will enjoy the material I've presented, as these discussions, I believe, are important to music. For those who want to learn more, I've included some introduction, though I suppose I'd recommend playing around with an instrument while reading. Even though I hope everyone who stumbles upon this will be interested, it's natural that the technical details of music won't interest everyone, so I hope those readers will feel free to skip over the those parts and perhaps discover something that is interesting in here.
SUMMARY
* Three main divisions of music creation are songwriting, performing and recording. Each has a different dynamic and different issues.
* Greatness and perfection are important concepts of the human mind. A thing is great if it arouses much pleasure in us and little pain. A thing is perfect if it arouses only pleasure in us and no pain.
* Music can exist at any level of greatness, and my belief is that in some senses music can be considered perfect.
* Music gives us pleasure are through harmony and rhythm, which are entirely mathematical concepts.
* Music also gives us pleasurable emotions which it elicits through permutations of harmonies, rhythms and lyrics. This could be considered a type of storytelling which is enjoyable to us.
* There are two fundamental "problems" with music: the "harmonic problem" and the "ratio problem."
The Harmonic Problem
* It is well known that at any point in time the sounds of musical instruments are made up of harmonics (simple sine wave tones) of various volumes. Each note consists of a fundamental tone, which is the frequency we focus on most, but also a virtually infinite number of tones are sounded along with this tone. Some are the same notes as the fundamental, some are related notes, some are different notes, and others are not notes at all.
* It is rarely discussed, but of all the harmonics emitted simultaneously by an instrument, some of them agree with the music and others sound dissonant with it.
* This is because each harmonic has a different frequency, and some of them have a good mathematical relationship to the music while others do not. Since there are often a virtually infinite number of harmonics in real world instruments, and their frequencies are dictated by the harmonic series, which is not always perfectly compatible with the ideal mathematics of music, dissonance is virtually always present. Instruments are considered more musical when the frequencies are partially organized into the intended mathematics of the music and the rest of the frequencies we generally ignore. Because of mathematical dissonances our experience of pleasure in "natural" music sometimes occurs with displeasure.
* The presence of many dissonant harmonics adds depth and realism to music. Paradoxically, we desire this realism, even though the harmonics actually conflict with music itself.
* With technology we can create sound "additively" with sine waves so that all the harmonics fall into the ideal mathematics of the music. Only such instruments can be considered harmonically perfect. But, value can still be found in natural instruments on a relative sliding scale. There was a time when I inspected these things closely, and I was frustrated with the imperfections of natural instruments. It took much analysis and education and ability in recording of both music and psychology before I was able to be enthusiastic about natural instruments again.
* There are two types of music, "perfect" and "imperfect," and imperfect music exists on a relative sliding scale of greatness. Virtually all sounds and music created today are the imperfect type because most music is created with natural instruments or electronic instruments which do not control harmonic content.
* In recordings the best way to balance realism and perfect harmonics, is to be very selective in the material used so that the mathematics of the music is showcased, and unmathematical frequencies are subdued. Usually this requires many recordings and focusing on one instrument at a time, for a long time, to find the best harmonic material. Harmonics in certain ranges and in certain situations are not likely to appear to conflict with the mathematics of the music. This process is a grey area and is often based simply on judgement of the person. The better executed the strategy, the more often the recording will be liked by listeners.
The Ratio Problem
* Throughout time we have found that a complex musical scale can not be made mathematically perfect.
* The more perfect we wish a musical scale to be, the more limited it must be in depth. I have found that all the notes of a pentatonic major scale of C(1/1), E(5/4), F(4/3), G(3/2), A(5/3) are sufficiently perfect in their ratios to all other notes of the scale. Similarly there is a perfect pentatonic minor scale, E(1/1), G(6/5), A(4/3), B(3/2), C(8/5). The inclusion of more notes into either pentatonic scale, though, would begin to introduce significant imperfections. However, the significance of the mathematical imperfections is relatively small and easy for listeners to ignore. To the human mind, the benefits of increased musical complexity generally outweigh the imperfections of complex scales.
It seems to me that the 7 note scale we use today can be thought of as an overlapping of 2 perfect pentatonic scales, CEFGA and GBCDE. The chord F is mathematically incompatible with the chord G. Therefore, using C and F in music takes the music one direction on the circle of fifths and using G and C takes it in another direction on the circle of fifths. This type of modulation between two relative pentatonic scales may be responsible in part for the tension and resolution of music.
* We often sacrifice perfection of a 5 note scale for the complexity, variety and possibilities that the 11 note western scale or other scales offer. Because the imperfections of the 11 note scale are so small, the brain can easily overlook them.
Psychology
* The human mind can ignore imperfections in music and focus on the the parts that are mathematically organized and such for a period of time. However, freedom from displeasure in natural music is not guaranteed. Partial pleasure though, is guaranteed. Some of the time we will experience pleasure, and some of the time displeasure.
* As humans our feelings of pleasure and displeasure oscillate in time often. Our perception can be warped such that even the smallest amount of pleasure seems to outweigh the displeasure. Or, our perception can be warped such that the displeasure seems to outweigh the pleasure.
* If when creating something we focus our minds on it, we use short term memory and become experts on the thing. After we step away from it, we lose those memories and we find that the thing seems better than we previously thought.
* With time and experience we generally become more discerning, notice imperfections and commit them to memory. Because of this, the value of recordings go down over time in our minds.
* For this reason I have considered a model of recording in which I first create a base recording of different parts, then save the material so that I can continue to work on the recording into the future so that they improve with time. If the recordings are improved throughout time, it is possible the songs will remain as good as I can make them.
This has the added benefit of my revisions being so precise and drawing upon so much material that the resulting recording should far exceed what would be expected.
* As listeners we must make the choice to value the pleasure as highly as we can. This ensures that we get the most out of life. For, in life we must withstand pain in order to seek the perfection of pleasure.
* A perfection of sound can be achieved through technology. Of course, a sliding scale between both natural and perfect sounds exists. But, for true perfection of sound to be achieved, the frequencies of the harmonics must be limited, therefore the timbre of the sounds that can be formed are also limited. Also, the notes of the scale might be also limited. Obviously, these limitations might be viewed as imperfections themselves.
The following text describes the above concepts and others in depth.
Music, like most subjects in life, is highly complex. As such, there may be many ways to frame a discussion about what the nature of music is. I will frame it in the way that I first approached it years ago.
I learned at a young age, that music can give us great pleasure. I experienced the pleasure and beauty of music to a high degree and I pursued music for a long time afterwards because of the profound effect it had on me. At that time I did not understand what the true nature of music is. The performances of experienced musicians or recordings on the radio were at a level that was extremely high compared to my level and ability to judge. Now I realize that I like all other young people was impressionable precisely because I was deficient in ability and experience. As such, some figures seemed wildly talented and possibly perfect in their musicianship to me. I wondered if I could some day acquire what they seemed to have. At this time sound timbre seemed to me to be a very important element of music. I loved the rich sustained sound that strings made. Looking back on it now I could say that my ears were not able to recognize anything beyond the large scale "objects" of guitar, note and chord. But, there was a world underneath, which would become clear to me.
Later I immersed myself in songwriting, performing, and recording. I found that each of these divisions of music creativity has a quite different dynamic from the others. Songwriting is creatively permutating intellectual ideas and harmonies and rhythms into new forms which tell a story. The ideas for songs can exist in our minds, they can also be represented symbolically in notation, and they can be performed. Performing is translating the intellectual ideas of songs into live music. Typical music performances are done imperfectly, and at different levels of greatness, and have the property that each is different from the next. Recording is translating musical performances into fixed form, so that they can be played over and over again. Often today, recording involves technologically combining the best of a number of performances. As I pursued these endeavors, I found that songwriting gave me much satisfaction, and performing was also good, but recording was the most problematic of all. For many years I struggled with my understanding of this. Many problems and questions presented themselves.
With experience in recording I became increasingly critical and my ears quite discerning. There was a time when I heard things in my recordings that I wished I wasn't able to hear. I became aware of an apparent flaw somewhere in the process and perhaps a little obsessed with understanding it and finding solutions. In part I regretted the sharpening of my awareness to this degree, but in doing so I knew I was actually longing for a perfection which wasn't real. I supposed that it is better to know the truth, even if that truth is not what I originally expected or hoped for. Also, I must consider that as an inexperienced youth, I was not perfectly happy either. I pushed myself to be better because I knew that I was not as skilled as those I admired. I wanted to be able to harness the power I observed in others, to invent my own artistic world of music.
After I investigated these things and learned many principles of music and psychology I took considerable satisfaction in my newfound knowledge. I believe that once the truth of these things is understood, accepting and enjoying that nature is easier to do. This principle is true of many endeavors in life. As we gain experience and knowledge, we start to see through the illusions, to ever greater levels of truth. And often, knowledge is power.
After this I investigated recording further and because of practice and experience, my ability increased to a level where I was more than ever able to influence the harmonics of recorded natural instruments. Since my ability increased, and my understanding of the psychological factors increased, I began to get more enjoyment out of the process of recording. I learned to balance the style and notes and programming of sound, which is a lot to balance so I am not surprised it took me quite some time to get to a point of creative power. I also learned that by being very precise and selective in my recording I can manipulate my own mind. I've recorded natural instruments over and over again, looking for the greatest raw material. However, this process does obey the principle of diminishing returns which says that the reward for increasing effort goes down over time. Still, the reward for repetition is real and significant to some degree as yet unquantified by me. The reward for focusing very precisely on the details, is that when I took steps back from the intense scrutiny and listened, short term memories are lost, and my mind enjoys what is heard more. Needless to say, others will generally not be nearly as critical of my recordings than I am, precisely because their minds are not nearly as experienced with my music as I am. It is of course, the same for all musicians and their music.
Music gives us pleasure through the technical elements of harmony and rhythm, which are mathematical concepts. The mathematics of the universe have a perfectness to them that is sought out and rejoiced in by humans. We find pleasure in any organization of the often unorganized frequency spectrum. We find pleasure in its mathematical closeness to perfection.
Music also gives us pleasure in the eliciting of emotional and intellectual responses in listeners through intellectually structured sequences of harmonies, and lyrics. The hopes and ideal situations that our minds are capable conceiving extend far beyond what we all are given in life. In music, people are allowed a freedom to create and exist in an intellectual world that has few limits.
While studying music I came across two musical problems, the well known ratio problem, and the lesser known harmonic problem. The ratio problem has to do with mathematical imperfections in the scales we use in music. The harmonic problem has to do with differences between sounds created by vibrations of musical instruments, and ideal harmonious sounds. The harmonic problem shows that virtually all instruments such as strings, drums and synthesizers emit combinations of harmonious sounds and dissonant sounds, which make them in one way, fundamentally imperfect. However, these problems and others I will discuss, are subtle ones. I will discuss them in detail, but it is not my intention to overstate the imperfections of music. It is my intention to state them exactly as they exist, while I reflect on the nature of music and human responses to it. As we all know, it is possible for one to enjoy music to a very high degree without even being aware of these technical things.
My analysis of the ratio problem naturally led me to thinking about the feelings music evokes. The section concerning music theory is a place where I have many more questions about what I found. I have been reading some about what others have found in the study of music theory and analysis of harmony. I still have much to learn, there is surely a great deal of research, but I've presented my initial thoughts on this interesting subject. The feelings we experience in harmony and rhythm appear to come from permutations of small integer ratios, and are highly controlled by a type of relativity.
Since I have framed my discussion around the fact that music creates pleasure and displeasure in us, I also discuss many psychological issues that define how we experience music. But, I must point out that what I have observed may or may not be identical to what others observe. Each of us is, after all, biologically different. However, we all share much in common, and it is my strong feeling that most of the things I've observed apply to the experiences of others.
It took me many years to learn the answers to questions I had about music. Organizing the ideas into this comprehensive writing has been a goal of mine and it has had the additional benefit of making them even more clear in my mind. I hope that others who are as interested in music as I have been, will find this writing helpful and interesting, if they should come across it. In the next sections I will attempt to explain what I learned.
GREATNESS AND PERFECTION
I believe that greatness and perfection are significant concepts to our psychology. When it comes to experiences, we might consider an experience to be great if it arouses much pleasure in us and little pain. We would consider an experience to be perfect if it arouses only pleasure in us and no pain. The distinction between greatness and perfection apply to an infinitum of human endeavors, and to music as well. I'm sure it is obvious that music is not always a perfect experience. Some of the time music gives us pleasure and sometimes great displeasure. But, when I was considering how great or perfect music can be to answer my own questions, I began to analyze the situation in greater and greater detail.
I first considered that the endeavors of life and music are highly complex. They are composed of numerous properties and qualities. When we think about them, as intelligent beings we are constantly trying to evaluate all these qualities and properties in our minds. Example properties of music might be timing and intonation. If all the properties of a song, performance, or recording, could be summed together, it might be simplistically viewed as existing somewhere on a scale of greatness.
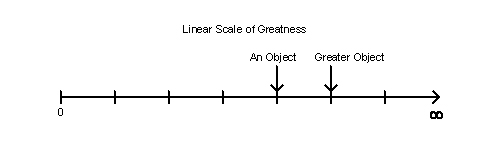
However, as with many situations in life, there is an inverse way to view this. We could say the thing is positioned on the scale closer to infinity by how "great" it is. We could also say the thing is also be positioned closer to 0 by how "ungreat" it is. Naturally, the if the properties of music are not perfect, this creates the opposite of pleasure, a displeasure.
THE RELATIVITY OF GREATNESS
It is common for people to talk about how "great" one song or performance or recording is in comparison to another. An interesting phenomenon though, is that sometimes people focus on differences in greatness that are very large, or differences in greatness that are very small, and sometimes not see the difference. I believe the reason for this is relativity. People's sense of the difference in greatness between two things only depends on what they are focusing on at the time. An example is if one person knows every detail of a certain musical genre, but another thinks it all sounds the same. Because these people have different levels of experience with the material, they perceive things quite differently and feel quite differently about it. Our perspectives are not fixed, but can change in time.
EVALUATING GREATNESS
In determining how to draw a scale of musical greatness, I considered the musical property of timing, which is easy to measure. In rhythm, events (such as the striking of a drum) which occur in small integer time ratios to each other give us pleasure. The symmetry of the time intervals excites the logical perfectionistic part of our psychology. For example, the most fundamental enjoyable musical rhythm occurs when the intervals are equal, having a 1:1 ratio between them.
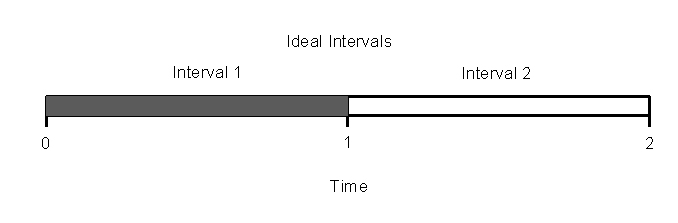
Of course, the ideal situation occurs if the intervals are exactly equal. It isn't important how long they are, just that they are equal. But, when any human performer attempts the ideal, the performer can not make the intervals exactly identical. There will be a measurable amount of error.
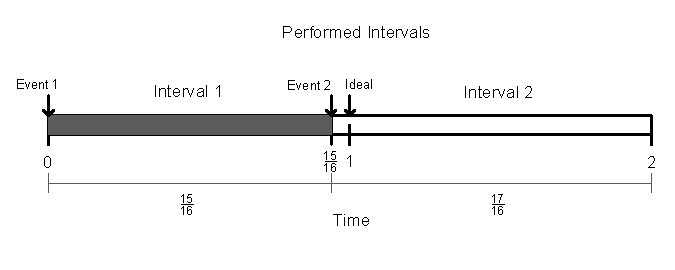
The amount of error can theoretically be calculated. In considering how to calculate this error, I reasoned that the error would be
> 0 if the intervals are equal
> infinite if one of the intervals was infinitely long in relation to the other
With this in mind, a simple scale of error can be constructed.
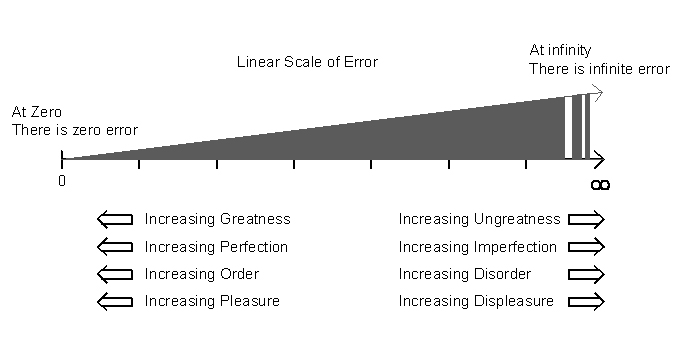
This scale represented the idea pretty well, but I wished to make a scale that is a distance between two points, 0 and infinity, so that both points can be viewed. So, linear and logarithmic scales were not sufficient. Instead, I've used what I'll call a sequential scale (because I'm not aware of any technical name for it). In order to graph things in this sequential graph, I used: y=h[f[g[x]]] where g[x]=Tan[x] and h[x]=Arctan[x]
I've graphed the error f[x]=x and its inverse, the perfection f[x]=1/x
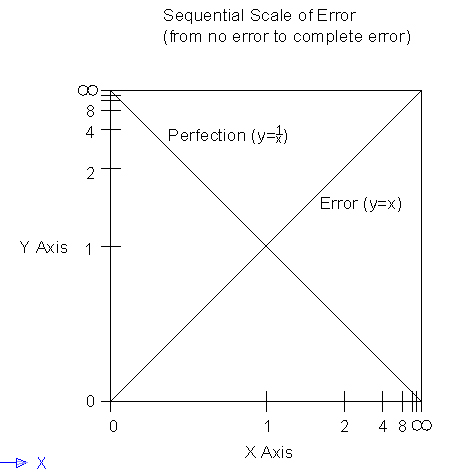
While I have had some significant experience in collegiate level mathematics, more experience would probably allow me to better explain what I've proposed in terms of number theories. It is an area of study I would like to investigate further because it seems that the concepts of zero and infinity are quite relevant to my discussion of perfection.
On the graph I've made, as the error goes toward 0, perfection increases rapidly. Perfection is achievable if the intervals are equal, but human performers can not achieve it. With technology, perfection in this property of music in recordings and types of live performances is practically achievable to a degree that exceeds the ability of the human mind to discern. This, I would say, is in all practicality an achievement of perfection if the human mind believes it is so.
In this writing I will show more ways in which the greatness of music can be observed, and potentially measured. However, the final effect, pleasure and displeasure, are ultimately psychological quantities, and as such may be complicated to measure. A listener's psychological values and biology may play a large part in determining how much pleasure and displeasure are felt.
SOUND
Sound comes from objects moving or vibrating in the physical world. The vibrations cause pressure changes in the surrounding medium of the air. These changes naturally travel outward in the shape of spheres of different pressure levels at the speed of sound. Pressure changes that are caused by objects that vibrate continuously for a time are called waves. In waves we find that the air is being sometimes in compression and sometimes in rarefaction. Waves can be visualized as "spheres" of compression and rarefaction emanating from the sound source. The pressure of the air therefore changes with time if the vibrations keep going. The pressure changes in the air are sound and can be recorded as shown below.
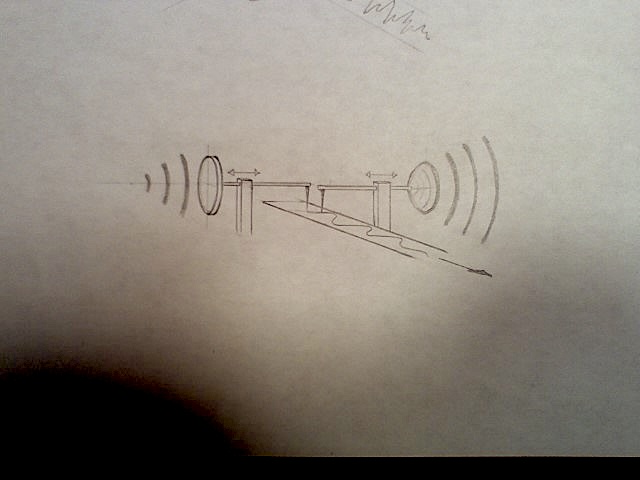
A simple phonograph microphone is affected by the waves sent by a vibrating object. The needle of the phonograph will transfer the waves to a two dimensional record. The original wave and the graph represent the same information. The wave is simply being represented in a new dimension. It is often difficult to understand that there is no two dimensional waving thing in the air. The picture of the wave drawn by the phonograph only represents the amplitude of the air pressure at different times.
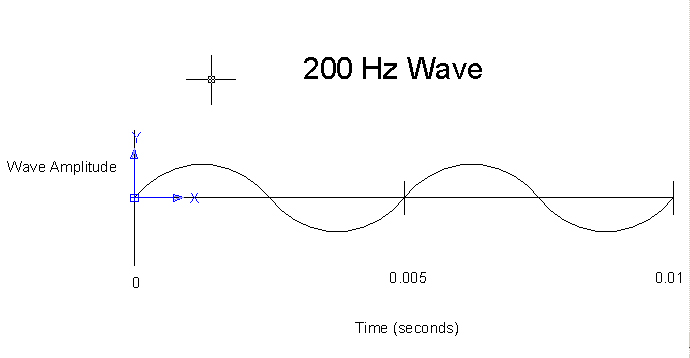
FREQUENCIES
The two dimensional record of a single perfect tone, is in a mathematical shape called a "sine wave." Sine waves are the simplest of all sounds and the building block for more complicated sounds such as music. Complex waves on the other hand, do not appear to have a mathematical shape. However, Fourier analysis can show that all waves, even the most complex can be decomposed into a number of simple sine waves. Interestingly, our brain can distinguish between superimposed frequencies quite well, especially with experience. However, the brain can not identify separate frequencies as perfectly as mathematical analysis can.
The pitch or frequency of any tone (the lowness or highness of its sound) is determined by how quickly in time the wave repeats its shape. Slowly repeating sine waves are very bassy or low sounding and quickly repeating ones are very shrill or high sounding. Sine waves alone can often sound even and pleasing to the human ear. However, a single tone is quite simple and without rhythm or changes in frequency or modulation of any kind would quickly become boring and would not be considered music.
The Hertz or (Hz) of a sine wave describing the pitch or frequency of the tone. Waves of any frequency can be produced. Humans can hear waves from about 20 Hz to 20,000 Hz. This is often called the sound spectrum because it is the range of frequencies where all perceivable sound exists. That sound spectrum can be full of any combination of frequencies. In a typical natural sound a virtually infinite number of frequencies are actually sounded all at once but at different volumes. The most dominant frequencies typically determine if there are notes and chords.
If a larger, more slowly vibrating object is recorded, the phonograph would record a lower frequency than the one above. The wave below repeats at half the rate of the above wave. Its pitch is perceived by the human ear to be lower than the above wave. However, these two frequencies have a special relationship because they are closely mathematically related.
Record imprints such as the above waves can be used to produce an identical sound in the speaker of a record player. It is simply the reverse of recording.
In music all notes are assigned to a specific frequency. For example, 440 Hz is always called an A.
RATIOS
If a 100 Hertz and 200 Hertz tones sounded at the same time, the phonograph would have to add them together (taking into account positive and negative regions). The resulting wave would look like the picture below.
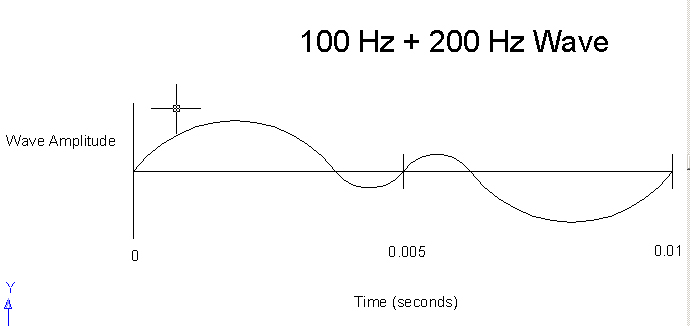
We would hear both tones simultaneously, and it is possible to mentally distinguish the two. Helmholtz may have showed that inside the ear there are structures that resonate with only specific frequencies, and this may be how our brain is able to identify single frequencies even when many are being sounded together.
Waves whose frequencies are in the ratio of 2:1 have a very important relationship in music. They are called an "octave." Both are thought of as the same note, but they do not sound exactly the same. One sounds higher in pitch than the other. However, they sound quite similar because their wave patterns repeat in a very mathematical way. An octave is a perfectly harmonious sound to the human ear because of the mathematical and physical relationship they have.
It is important to note that it doesn't matter what one of the frequencies is. They could be
200 Hz and 100 Hz
440 Hz and 220 Hz
360 Hz and 180 Hz
or any frequencies that are related by the ratio 2:1
Only their relation to each other matters. General rules for how frequencies will sound together might be:
1. If the ratio between two frequencies is a fraction made composed of small integers then the frequencies will sound good together. 2. Because of the existence of octaves and the associated mathematics, if 2^n (where n is any integer) can be subtracted from the fraction to form a small integer fraction then this indicates frequencies that will also sound good together. They may be separated by a number of octaves, but no matter what octave a frequency is played in, it is still fundamentally the same note as all the other octaves.
For example:
3/2 is a good ratio because it is itself a small integer fraction.
7/3 is a good ratio because 2^1 can be subtracted to form 1/3, which is a small integer fraction.
8/5 is a good ratio because 2^0 can be subtracted to form 3/5, which is a small integer fraction.
3. The pureness of the relationship seems to depend on how small the resulting integers are. Perhaps a multiple of them (top integer x bottom integer, or some similar mathematical operation might provide a way of evaluating their ability to please the ear)
For example:
1/1 would be the best ratio because it is what is called a "unison," the same note
1 x 1 = 1
7/3 reduces in this system to 1/3
1 x 3 = 3
8/5 reduces to 3/5
3 x 5 = 15
So, two waves whose frequencies are related by these small integer ratios tend to sound most pleasing to the human ear. This seems to be related to the fact that the intervals in which the waves repeat coincide in an even rhythmic manner. Waves with small ratios often form nice repeating patterns when summed together. But, if we combine too many different notes or notes of large number ratios, the symmetry will be lost and the chord will generally not sound good.
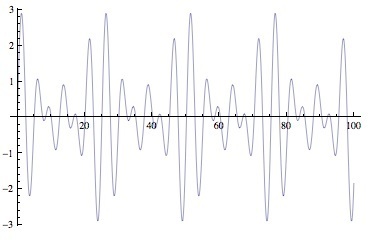
A pleasant wave is still ordered
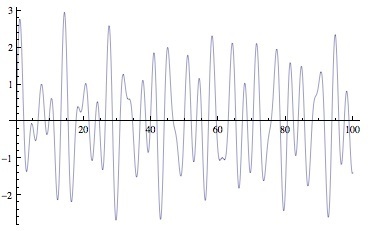
An unpleasant wave is much more random
SCALES
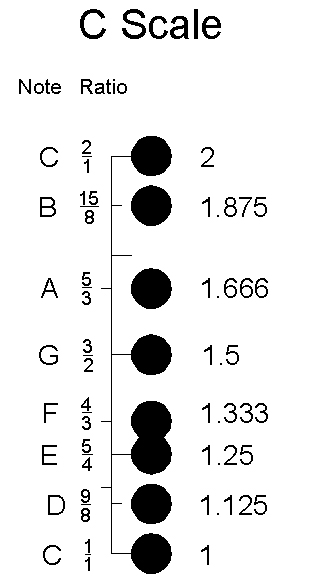
The frequencies of most of the waves below are in small integer ratios to C1. These notes make up part of what could be a basic scale of music. Whether or not these are ideal ratios, I will discuss later. The way I will write ratios is the ratio given is the frequency of the note divided by the frequency of the note I am comparing it to (in this case, C1).
Note Ratio
C 2.000 2/1
B 1.875 15/8
A 1.666 5/3
G 1.500 3/2
F 1.333 4/3
E 1.250 5/4
D 1.125 9/8
C 1.000 1
The scale repeats after C2 with the same notes, but in a different octave. Frequency is an exponentially growing number because each successive octave requires a doubling of frequency.
Note Ratio
C 4.000 2(2/1)
B 3.750 2(15/8)
A 3.333 2(5/3)
G 3.000 2(3/2)
F 2.666 2(4/3)
E 2.500 2(5/4)
D 2.250 2(9/8)
C 2.000 2/1
B 1.875 15/8
A 1.666 5/3
G 1.500 3/2
F 1.333 4/3
E 1.250 5/4
D 1.125 9/8
C 1.000 1
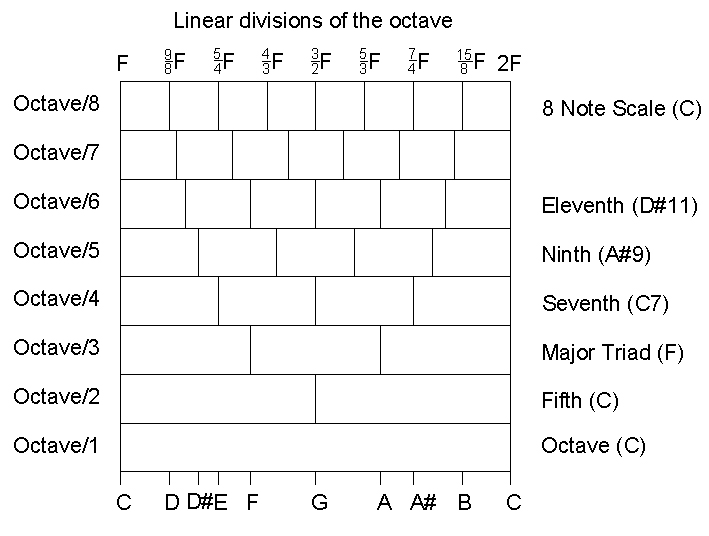
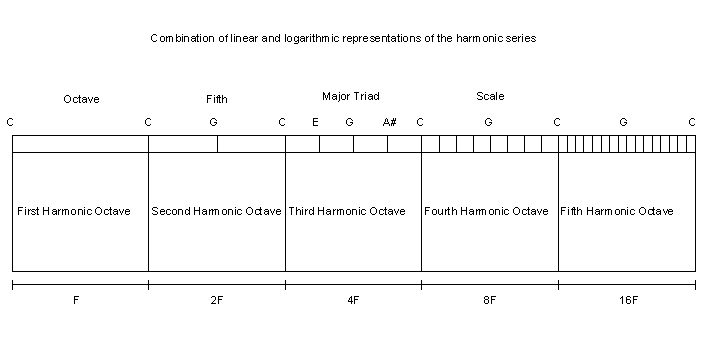
Because the frequencies of the scale grow exponentially, graphs of notes can be represented either linearly or logarithmically. When showing ratios I've usually represented the frequency based distances between notes linearly, but at times when an illustration spans several octaves, it is more practical to represent frequencies logarithmically. In the picture below, the distances are linear.
During my search for perfection in sound, I examined these ratios in considerable detail. The actual ratios used in musical scales have been experimented with and debated throughout history. This is because of the problem of ratios and the limitations of historical real world instruments. The mathematician Pythagoras is credited with the discovery of musical ratios and the problem of ratios. Today our standardly accepted equal tempered scale uses ratios that are close to the above, but not these exact ones. What we use today is an approximation which has practical reasons.
There are two ways in which we understand musical information. I'll call these chords and sequences. Perhaps there are other technical names for them. Chords are when two or more notes are sounding simultaneously, and the ratios between them evoke a feeling in listeners. Sequences occur when there is a transition from one note or chord to another, which can also evoke different feelings in listeners. Interestingly, a sequence can give a feeling to a chord, which isn't inherently in the chord itself. A single chord is a pretty basic concept, but sequences are much more dynamic.
CHORDS
Chords are a combination of notes. They can be beautiful, but are not often by themselves be considered music. Generally, sequences are music, and chords are the building blocks of sequences. Interestingly, different combinations of notes can evoke different feelings in listeners.
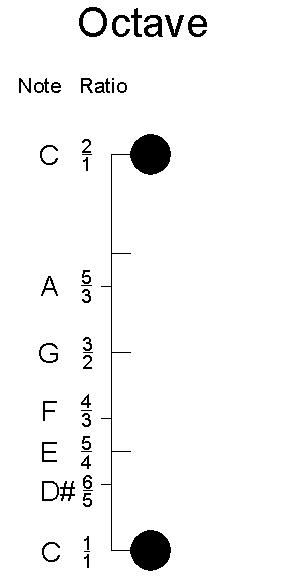
The octave sounds very basic. Because no other notes are being sounded, the listener does not have much information with which to interpret this sound.
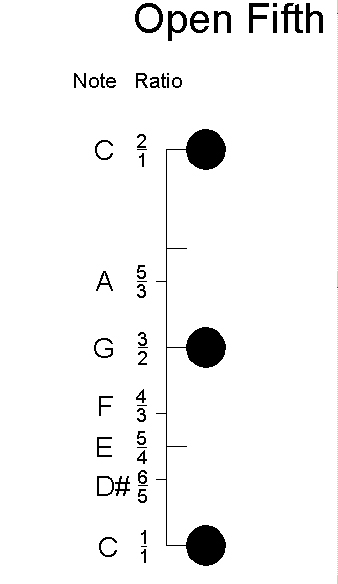
An open fifth evokes an airy feeling. This is because other notes of the chord are not present, so it sounds open, undefined and ethereal.
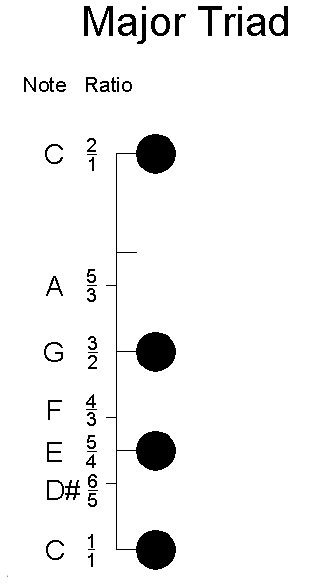
A major triad is a very harmonious, bright, positive and pure chord. Even though it doesn't show on this diagram, another way of looking at the major triad is it is the linear division of the octave into three equal parts. From the above perspective it appears the octave is divided into four parts where the A# note is absent. It seems this is all part of the beauty of the mathematics of these ratios, and the beauty of harmony. The ratios of a major triad are:
C 6/5(times A)=6/3(times C)
A 5/4(times F)=5/3(times C)
F 4/3(times C)=4/3(times C)
C 1/1(times C)=3/3(times C)
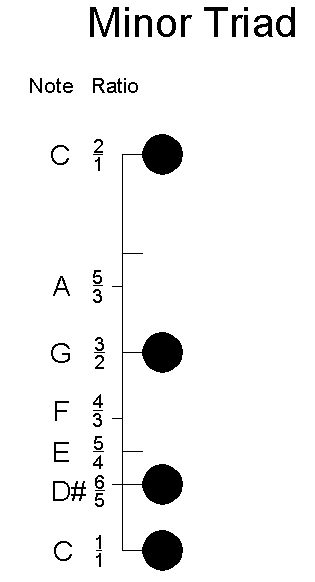
A minor triad is the dark and moody opposite of a major triad. The ratio structure of the notes is slightly different than in the major triad. A diagram of the harmonic series reveals that the minor chord does not exist in sequence, but does exist spanning octaves.
C 4/3(times G)=2(times C)
G 5/4(times D#)=3/2(times C)
D# 6/5(times C)=6/5(times C)
C 1
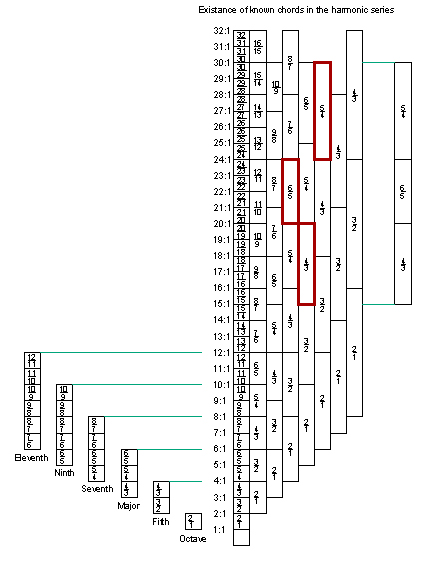
The major triad and the minor triad are the only two different combinations of the ratios (4/3,5/4,6/5) possible. They are the simplest chords after the fifth (4/3, 3/2) and octave (2/1). These two chords seem to represent two extremes in human moods and this may reflect something significant.
It can be observed in this chart of the ratios in the harmonic series, that the ratios we use for chords can be found within the series.
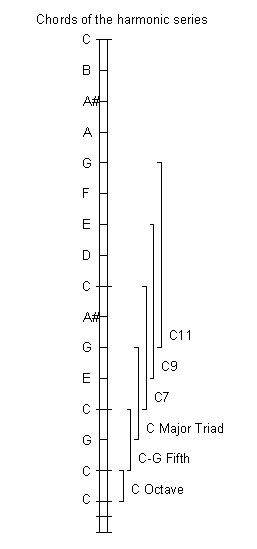
Often it seems the nicest formation of a major chord can be defined by this arrangement of ratios, (1/1,2/1,3/2,4/3,5/4,6/5). These makes a fairly spread out major chord which is a very common formation in classical piano music. Interestingly, this mathematical arrangement of ratios and frequencies corresponds to the harmonic series of real world instruments. The frequencies of the notes can be found by a product series, where each note is multiplied by the next ratio in the set. For example, if the starting note was 100 Hz, then the chord would be made up of the following frequencies:
600 (6/5 times 500)
500 (5/4 times 400)
400 (4/3 times 300)
300 (3/2 times 200)
200 (2/1 times 100)
100
Other chords and feelings are possible when more or different ratios are used. For example:
2/1 (octave)
4/3,3/2 (fifth)
6/5,5/4,4/3 (minor)
5/4,6/5,4/3 (Major)
5/4,6/5,7/6,8/7 (seventh)
6/5,5/4,7/6,8/7 (minor seventh)
6/5,7/6,5/4,8/7 (minor 6th)
5/4,6/5,10/9,6/5 (major 6th)
SEQUENCES
A sequence of notes or chords in discrete time intervals is music. I will start by describing sequences of notes, or melodies. In the musical scale below, the fundamental building block of the scale is the note or frequency of C.
Note Ratio
C 2.000 2/1
B 1.875 15/8
A 1.666 5/3
G 1.500 3/2
F 1.333 4/3
E 1.250 5/4
D 1.125 9/8
C 1.000 1
If we play any random sequence of these notes, it can be observed that each note has a particular feeling to it. Now this is strange, because where before a note by itself was just a tone, now it is taking on a character. This must be because our memory recognizes the ratios being employed in a sequence, even when notes are not sounding simultaneously.
In a C scale,
B also has a feeling of preceding finality. This note is highly suspenseful. The melody wants to be resolved by going to C
A has a darker feeling, but also a feeling of finality. There are reasons for this.
G has a feeling of preceding finality. It is suspenseful. The melody wants to be resolved by going to C next
E has a feeling of beauty and perfection but with a little hint of suspense
D has a strong feeling of suspense. It is located right next to C
C has a feeling of finality. It is the root, or most important note in the scale.
Each note in a scale has a character that can be recognized. A trained musician can identify a note's place in a scale simply by hearing a sequence of notes.
Using these notes, we can also form major and minor chords that fit within the scale.
An important chord is the C major triad, CEG. Another important triad in the C scale is the G chord, GBD. Notice how the G chord contains notes which are in between the notes of the C triad. Each of the notes of the G chord are suspenseful. Naturally, the G chord has a sound of being unresolved and tense. The relaxing of this tension occurs when the C triad is sounded.
It is interesting that even though both of these chords have identical ratios in all their notes, and identical feelings when sounded alone, they can be made take on quite different feelings in a sequence.
The F triad, FAC, is also a very important chord to the C scale. All of its ratios have the exact same proportions as the C and G chords. The Am triad, commonly referred to as the relative minor of the C scale, too is a very important chord. Because Am contains the fundamental note C and a note of the C triad (E), it is the minor chord which carries a sound of finality in the key of C.
The chords are:
CEG
DFA
EGB
FCA
GBD
ACE
THE RATIO PROBLEM, RELATIVITY AND MODULATION
In the next couple sections that relate mathematics and music theory, I'm still working and unsure about my conclusions. I've commented on how mathematics seems closely related to the scales and modulations we use in music.
From here on I will use the term interval to describe a combination of two notes. The ratio of the interval is the ratio of the higher note divided by the ratio of the lower note. For example, the interval between G and E is (3/2)/(5/4)=6/5.
Based on mathematics, here is a scale of notes I'll call the C-F Pentatonic Major Scale. I've included the ideal ratios of these notes to C.
C-F Pentatonic Major
C - 2.000 2
A - 1.666 5/3
G - 1.500 3/2
F - 1.333 4/3
E - 1.250 5/4
C - 1.000 1
Notice that this scale does not yet include the typical notes D and B. D and B can only form perfect intervals either with G and E, OR F and A. They can not agree mathematically with both. The discrepancy is one way of illustrating the problem of ratios. Another way is through the circle of fifths shown in another section.
B must be 17/9 above C to sound perfect with F and A.
B must be 15/8 above C to sound perfect with G and E.
D must be 10/9 above C to sound perfect with F and A.
D must be 9/8 above C to sound perfect with G and E.
The difference between 10/9 and 9/8 relatively speaking, is greater than the difference between 15/8 and 17/9. Historically, the second note of the scale has been a point of big debate. At one time, a scale called the meantone temperament averaged the difference between the two and called that frequency the second note. Obviously, this was an imperfect but practical solution.
It follows that mathematically the two notes G and E, are slightly incompatible with the two notes F and A. They share good ratios with only one other common note, the note of C. I will propose that this could be why C is the fundamental of the scale. I will also propose that the notes G and E take a sequence in one direction, and the notes F and A take it in another.
PERFECT SCALES
The interesting thing about the ratios below is that, mathematically their notes can form the simplest and most perfect harmonious intervals. The five distinct notes could be called a pentatonic scale, although the ratios are different from many historical pentatonic scales. Tasteful sequences of notes of these two scales certainly have the potential to be flawless in their mathematical harmony. This is because not only does each note form a small integer ratio with the fundamental C, any combination of them, also forms an acceptably small integer ratio.
C-F Pentatonic Major
C - 2.000 2
A - 1.666 5/3
G - 1.500 3/2
F - 1.333 4/3
E - 1.250 5/4
C - 1.000 1
This scale is includes chords C, F, and Am
Am-Em Pentatonic minor
E - 2.000 2
C - 1.600 8/5
B - 1.500 3/2
A - 1.333 4/3
G - 1.200 6/5
E - 1.000 1
This scale includes chords Em, Am, and C
These are the two separate scales that I have found to have the best ratio relationships. As far as I know, any scale of ratios other than the ones above will be significantly less perfect than these, and any other notes added to them will make them mathematically less perfect. If another note was added, it would have the potential to form a good interval with some notes, but would form a significantly dissonant interval with at least one other ratio. For example, 6/5 (D#) might be a good candidate for the C-F Pentatonic Major scale, but in examining its relationship to the other ratios, its interval with A is (5/3)/(6/5)=25/18. Another possibility for the C-F Pentatonic Major scale might be an A# with a ratio 7/4, but A#'s interval with F is 21/16. F and A# would be best when in a simple 4/3 interval.
The supremacy of the above ratios, I believe, is critical to any discussion of an ideal musical scale. Notice that when using the above ideal ratios of the Pentatonic Major scale, there can really only be three distinct triads.
If we were less ambitious and less imaginative, the chords and harmonies made up from the perfect five ratios would be enough for all of music. However, throughout history, people have desired more.
RELATIVITY
As I mentioned once before, the F chord is an exact transposition of the C chord in that the ratios of the F chord are the same ratios used to form the C chord. The only difference between them is that the starting frequency of an F chord is higher (4/3 times the starting frequency of a C chord). I call all these notes the C-F pentatonic scale.
----C--
--------
----A--
G------
----F--
E------
--------
C-------
The same is true of F and Bb. Now F takes on the fundamental role and a chord with new frequencies is introduced. I call this the F-Bb pentatonic scale.
--------F--
------------
--------D--
----C------
--------Bb-
----A------
------------
----F-------
-----------
-----------
C----------
Not surprisingly, inspection of this new pentatonic scale reveals that the notes form good ratios with F, but not with C.
Ratio Ratio
To F To C
F 2/1 8/3
D 5/3 20/9
C 3/2 2/0
Bb 4/3 17/9
A 5/4 5/3
F 1 4/3
D 5/6 11/9
C 3/4 1
MODULATION
Knowing that F is 4/3 above C, and that C is 4/3 above G, hopefully by now it is clear that C is to F as G is to C. The C chord is closely related to both of them.
F
C
G
In sequences of F, C and G chords, C becomes psychologically the strongest most fundamental chord, and I propose an F chord takes the music in one direction, and a G chord takes it in another. As I have shown, an F chord and a G chord are a step away from each other mathematically. Furthermore, I will propose that what is referred to as the "C scale" may be described as a combination of two of the ideal pentatonic scales I described above. In the case of the western "C scale", we have two pentatonic scales combined and overlapping, C-F and G-C.
F-Bb Pentatonic
To F To C
F 2/1 4/3
D 5/3 10/9
C 3/2 1
Bb 4/3 17/9
A 5/4 5/3
F 1 4/3
C-F Pentatonic
C 2/1
A 5/3
G 3/2
F 4/3
E 5/4
C 1
G-C Pentatonic
To G To C
G 2/1 3/2
E 5/3 5/4
D 3/2 9/8
C 4/3 1
B 5/4 15/8
G 1 3/2
All the scales above are relatively identical to each other, built on different frequencies. Adjacent scales such as F-C and C-G are very similar in their notes. If we start with the triad CEG, and add the notes for an F chord, we've defined this scale as being an C-F scale. We can't then introduce the notes for G without a slight redefinition of the scale as a G-C scale. So, if we use F, it seems to take the modulations of the music in one direction, and if we use G, it seems to take the modulations of the music in the other.
A simpler way to illustrate modulations
Chord in the circle Possible keys the chord could appear in
Ab / Fm (Eb)
Eb / Cm (Bb) (Eb)...
Bb / Gm (F) (Bb) (Eb)
F / Dm (C) (F) (Bb)
C / Am (C) (G) (F)
G / Em (C) (G) (D)
D / Bm (G) (D) (A)
A / F#m (D) (A)...
E / C#m (A)
B / G#m
F# / D#m
C# / A#m
This is a representation of a circle of fifths, which is discussed again below. It is my feeling that any time we play combinations of chords that are not in an ideal pentatonic scale together, it is inherently a type of modulation, and for some reason, the modulation is what really gives music its quality of tension and resolution. I do not believe that music played inside a single pentatonic scale evokes nearly as much tension and resolution in our minds as music which uses more than one of these scales.
WHICH CHORD OF A TWO CHORD PENTATONIC SCALE IS THE FUNDAMENTAL?
It can be difficult to tell from sequences of a C-F pentatonic scale, which chord, C or F, is the root. Both C and F have a quality of finality to them.
The C-F pentatonic scale allows us to play the A minor chord, which is closely related to C. By this psychological clue, we are disposed to think that the scale is C and not F. There may be other clues, but I haven't been able to form a conclusion. I believe that no fundamental can really be named without modulation to either F-Bb or G-C as described above. Modulation, therefore, may be what tension and resolution in music is really about.
It seems that in a 7 note western scale, the mathematically pure pentatonic scales of F-C, G-C are overlapping simultaneously If you look closely, and know the size of the steps between the notes, you can see clear analogies in the notes CDEF and GABC,
THE PENTATONIC MINOR SCALE
I did not examine the pentatonic minor scale as closely as the pentatonic major scale. However, the same process would hold for the modulation of an Em-Am pentatonic minor, to an Am-Dm pentatonic minor, or to a Bm-Em pentatonic minor.
Em-Am Pentatonic minor
E 2/1
C 8/5
B 3/2
A 4/3
G 6/5
E 1
Am-Dm Pentatonic minor
Ratio Ratio
to A to E
A 2/1 - 8/3
F 8/5 - 8/5
E 3/2 - 2
D 4/3 - 10/9
C 6/5 - 8/5
A 1/1 - 4/3
F 4/5 - 16/15
E 3/4 - 1
I've talked extensively about the C G chord sequence and how it creates a feeling of tension which the human mind wants to put back into order. The mind seems to want to designate the chord which is connecting two relative pentatonic scales the fundamental chord. Another very common chord sequence which generates the same feelings is of course, the C minor - G major sequence. This may be a similar modulation, but from a Gm-Cm pentatonic minor scale, perhaps to a G-C pentatonic major
Cm-Fm Pentatonic minor
C 2/1
G# 8/5
G 3/2
F 4/3
D# 6/5
C 1
ATTEMPTS TO FIX THE MATHEMATICS OF THE RATIO PROBLEM
So, it turns out that very nice tonal music could be made out of a single pentatonic scale that never modulates. But, we would miss out on all the variety and richness that modulation makes possible. As I hope I have shown, the 7 note western scale can not be made mathematically perfect without a redefinition of the notes used. How much redefinition needs to happen depends on how far we stray from a single major pentatonic scale.
There are ways to achieve frequency reassignment of notes instrumentally or electronically. There are also historical methods of mitigating this problem. In my own attempts to rectify the problem, I found that it is not complicated to program digital instruments to change intonation based on the scale being played. I see that there are many commercial musical products which claim to employ similar processes for midi instruments, but achievement of harmonious perfection in a 7 note scale is not without problems. The logistics of redefining note frequencies becomes quite complicated and in some cases it may be impossible to achieve simple mathematical harmony. Also, changes in note definitions of a 7 note scale can be perceived by listeners. I have started to experiment with this in my final song of The Romance of the Strings. I'm not sure if it is preferable to shift frequencies or is it better to leave the notes as fixed ratios that are only slightly off. I plan to experiment with this more in the future.
EQUAL TEMPERAMENT
Equal temperament is a very close approximation to the ideal musical scale.
Just for fun, to illustrate the problem of ratios further, I could find a circle of fifths by multiplying the fundamental C1 by 3/2, and then doing it again and again to find relative fifths. This was supposedly done by Pythagoras, and he discovered a problem.
If the simple ratio of 3/2 is used to create a circle of fifths, the ratios can never reduce back to simple fractions because 2 does not go into 3. The discrepancy we find between (3/2)^12 and 2^7 is very small, but significant and it has been termed the Pythagorean comma.
F7(177147/2048) * 3/2 = C8(531441/4096)
A#6(59049/1024) * 3/2 = F7(177147/2048)
D#6(19683/512) * 3/2 = A#6(59049/1024)
G#5(6561/256) * 3/2 = D#6(19683/512)
C#5(2187/128) * 3/2 = G#5(6561/256)
F#4(729/64) *3/2 = C#5(2187/128)
B3(243/32) * 3/2 = F#4(729/64)
E3(81/16) * 3/2 = B3(243/32)
A2(27/8) * 3/2 = E3(81/16)
D2(9/4) * 3/2 = A2(27/8)
G1(3/2) * 3/2 = D2(9/4)
C1(1) * 3/2 = G1(3/2)
So by this method, C8 = (3/2)^(12) = 3^(12)/2^(12) = 129.7463...
However, the ideal ratio for C8 is of course 2^7 = 128, an exact octave of the original C1.
Many classical instruments such as pianos could not change their tunings from key to key. In order to allow modulation among all the 11 keys, an imperfect compromise was made. The equal tempered scale uses a logarithmic approximation to correct for the Pythagorean comma. Instead of an exact 3/2, a ratio of 2^(7/12) = (1.498307...) is used. When the notes are calculated logarithmically, the frequency of each note ends up being 2^(n/12) where n is the number of the note from 0 to 11. The equal tempered scale is a good compromise because it naturally comes close to ideal ratios, corrects for the Pythagorean comma.
Logarithmic Ideal Ratio
Approximation
C 2.000 = 2^(12/12) 2.000
B 1.888 = 2^(11/12) 1.888 or 1.875
A 1.682 = 2^(09/12) 1.666
G 1.498 = 2^(07/12) 1.500
F 1.335 = 2^(05/12) 1.333
E 1.260 = 2^(04/12) 1.250
D 1.122 = 2^(02/12) 1.111 or 1.125
C 1.000 = 2^(00/12) 1.000
How significant the problem of ratios is, depends on how complex the music is, and how closely one is listening. As is a common theme, the more complex the composer wishes to make the music, the more error is introduced. The problem of ratios has not been as significant in music to me personally, as is the next problem I will discuss. For complex instrumental music which modulates, and for instruments with fixed tunings such as piano and guitar, an equal tempered scale may be the best option. All the best harmonies in the universe are represented in the equal tempered scale. The imperfections of scales are small and often unnoticeable to listeners.
HARMONICS
Now, as it happens, most objects in the real world that vibrate don't emit only one single sinusoidal tone. Vibrating objects physically emit a virtually infinite number of tones at many different frequencies. And, the frequencies that are given off by many natural objects happen to be good ones mathematically. The more musical an object is, the more this will be the case, but even the most musical real world instruments have very large numbers of harmonics at many different frequencies.
Harmonics happen because natural vibrations aren't simple and one dimensional. They are many partial vibrations. A string, for example, is fixed at two ends. It will vibrate back and forth at a fundamental frequency, but it forms nodes at integer divisions of the string. Nodes can only occur in specific places. At each section between the nodes there is a partial vibration, creating a harmonic. This system continues on virtually forever, and it is called the harmonic series.

As there are many harmonics, there are many different possible combinations of volumes of each harmonic. Their volumes depend on how the object vibrates physically. Usually the volume of the harmonics goes down at higher frequencies. The harmonic content of any sound gives it its own unique character. This is why a string, a horn and a human voice all have different sound character, even when they are vibrating at the same fundamental frequency.
Out of all these emitted frequencies, the tone that has the strongest volume is the fundamental. All the rest of the tones are harmonics. The harmonics of a stringed instrument such as this actually are very mathematical. The harmonic series is shown below
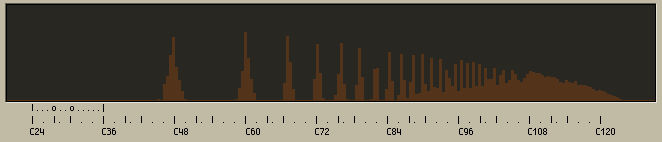
Harmonics of notes follow the simple mathematics of the harmonic series. The first few frequencies given off by a C note are C, C, G, C, E, G, A#, C... with the first harmonics being the loudest. Therefore, a note of C on a real instrument subtly suggests a C chord itself. When we play the note of G, we hear its harmonics. The G is simply a C transposed up to the frequency of G, because the physical world isn't aware of scales. We hear the harmonics G, D, and B, which make up the G chord. Thus, a note of G subtly suggests a chord of G.
Knowing that the human ear is capable of frequency separation, and that harmonics are a phenomenon of real world instruments, you have enough information to understand a second fundamental problem in music. While the most beautiful combinations of tones are in ratios such as a 2/1, 5/4, and 3/2, you can see that many of the tones even a single string produces do not fall in the ratios of an ideal chord. However, most listeners do not notice this because the good fundamental harmonics are the loudest and most prominent. But, upon closer investigation, the reality can be heard. After the first few harmonics of a C note, there are Ds, Bs and harmonics that do not even fall on notes of the scale. The symmetry of this wave is thus slightly confused. Its beauty is ironically marred by the richness of its harmonic content. The notes of real world musical instruments are more perfect than most earthly sounds, but there can be no doubt that they are fundamentally imperfect.
As I have stated before, the human ear is capable of frequency seperation. The human brain can hear a complex wave and filter out the harmonics all on its own, though it sometimes takes a little experience to understand this ability. Since I have been involved in music for many years, my ears do this with great ease, which has over the years been a source of great frustration.
When I was younger I experienced a time when the tone of a piano seemed perfect, when the sound of a guitar was heavenly, when a drum was just a drum. I was able to intellectually connect directly to the ideas being conveyed in music. I did not have any concept of harmonics. Naturally, I observe that people who have not engaged in studio engineering as their hobby do not generally notice them either. They respond to music on different psychological levels which I talk about later in this writing. As for myself, after I began to study the science of recording in an effort to make music myself, I became aware of this phenomenon. After I understood the physics of the situation, I began to take a closer look at the psychology of music.
QUESTIONS OF SCIENCE AND PSYCHOLOGY
When I was first engaged in my study of sound I was inexperienced at it. It took me many years to make sense of my observations. At first I thought the harmonic dissonances I was hearing on my recordings must be due to flaws in the recording equipment. I didn't hear them in the music while I was playing. The reason for this was entirely psychological and it is something I will explain. Eventually I learned that my equipment was reproducing the stringed instrument sound accurately, and it was the stringed instruments that were flawed, but I wondered why recordings on the radio sounded so perfect to me, and how this was achieved. The answer to this again turned out to be psychological in nature. Other recordings weren't perfect either, but I couldn't hear the flaws as easily.
During my experiments I wondered what was possible. Is perfection in music possible? If so, what would be the nature of perfect music? Could the instruments of the natural world be altered somehow to sound perfect or better? What are the psychological principles at work here? I questioned many things, and I think I can now offer a few interesting observations and conclusions.
PERFECTION IN MUSIC
After much experimentation and thought, I was persuaded to conclude that there is one type of perfection possible in sound, a combination of sine waves which fall into the intended chord in the sequence. Sine waves are the only sounds which can be strategically placed into the harmonic ratios without creating harmonic dissonance. And as I discussed in the section on the problem of ratios, perfection even with sine waves has subtle limitations.
Sine waves can be shaped to make a variety of different timbres such as organs, bells, wooden sounds, and others. However, they can be percieved as limited in the richness of their character by their lack of imperfect harmonics, especially when compared to more harmonically indulgent music.
If music contains samples of real world instruments, the human voice, or geometric waveforms other than sines, then it will surely have harmonics which don't belong to the chord. In that case the music enters a grey area which is not exactly perfect, but can still be close. I will discuss different types of perfection and imperfection in the next few sections.
ATTEMPTS TO FIX THE HARMONIC PROBLEM
In my youth I attempted many methods of rectifying the problem of dissonant stringed instrument harmonics. The first method I tried, filtering or "equalization," was much like hitting my head against a wall. Filtering uses Fourier analysis of a wave to raise and lower ranges of frequencies in the sound spectrum.
Harmonics of a mathematical "saw wave," which contains all the harmonics in the harmonic series.
The filtered "saw wave"
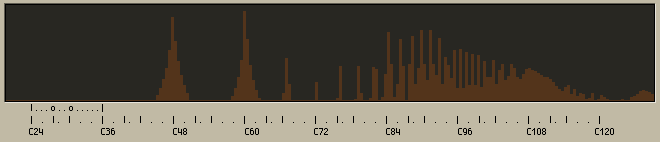
It is possible to narrow the range significantly and only cut out some offensive harmonics, but this affects the quality of the sound by also reducing good harmonics. What I found in filtering, was that one can cut the frequencies until a sound is reduced to virtually nothing, but the harmonic content is simply intrinsic to the sound. Just by looking at the series of harmonics that a real world instrument emits, it should be obvious, that they can not all be removed, especially since the frequency related distance between harmonics decreases the higher up we go in the frequency spectrum.
One interesting idea I came up with was what I called a resynthesizer. It analyzes the amplitude of each frequency of an input signal, and creates nearby sine waves (on good harmonics only) that follow the amplitude of the nearby harmonics. This, as one might expect, does not end up sounding like a real world instrument because the harmonic content has changed so dramatically.
The best instrument I ever created was intended to make perfect sound. It is a sine wave generator which creates harmonics above the intended note one by one, and only harmonics that are in the chord being played. I was able to make this instrument follow a more correct mathematical tuning. A recording which features this instrument is my last track of "The Romance of the Strings." The recording could have been developed a lot more, but it was not necessary to illustrate what approaches "perfect music." I decided to save the creative embellishments for a future electronic record. I have found that I personally am more relaxed and consistently pleased by my sine wave music than I am by any of my real world instrument productions.
GREY AREAS
I believe that any time harmonically imperfect sounds are introduced into a recording, a grey area is entered. Judiciously introducing sounds, whose dissonant harmonics are minimal has the potential to improve the richness of these recordings with a loss in purity that is negotiable. The following describe some grey areas.
NOISES
Noises have some merit because they have an equal and large amount of harmonic content in whole ranges of frequencies, but I have noticed their random harmonic content can easily become distracting to harmony, so I would have to designate them as less than perfect.
THE HUMAN VOICE
The human voice is well behaved harmonically. Its dissonant harmonics are often very subtle, but it is still a natural instrument.
CLASSICAL INSTRUMENTS
Classical instruments such as the piano and bowed instruments often have significantly muted higher frequencies, but as they are stringed instruments, they can not be absolutely perfect.
ORGANS AND BELLS
It is interesting to observe that perfectly constructed instruments bear similarity to certain real world instruments, namely organs and bells. However, real world organs and bells do not necessarily have perfect harmonics.
LEAD INSTRUMENTS VERSUS MULTIPLE NOTES
Consider the second harmonics of a major triad, CEG. The first harmonics are CEG. The second harmonics are the notes GBD. The note B especially is problematic because it is a very tense note when sounded with C, as it resides right next to C. I have found that instruments which are played monotonically, have harmonics that are more easily tolerated than chords.
SPEED VERSUS SUSTAIN
Musical passages that transition quickly make it unlikely that listener will be able to identify harmonic dissonances. On the other hand, sustained passages that are repetitious in their percussiveness such as repeated sustained guitar and piano chords, sometimes make it more likely that harmonic dissonances will be identified.
BASS INSTRUMENTS
The harmonics of bass instruments are often not objectionable because they are often quieter, and occur at low frequencies where the ear seems to be less sensitive to subtlety.
DISTORTION
Another method I worked with was the use of heavily distorted sounds. Distortion and noise are closely related. And, as I said above, noise is somewhat of a pseudo-perfect sound because it contains non-tonal harmonics. Distorted guitars have a great deal of haphazard harmonic content mixed with their noise. They also have a great deal of good harmonics which gives them their appeal. Because there are so many dissonant harmonics and the sound isn't as clear as an acoustic string, I have found them generally more pleasing, but not perfect.
PERCUSSION
Percussion sounds have a great degree of noise in them, and harmonics that occur at some strange frequencies. They are capable of a perfections of rhythm. Technology has made it possible to create intervals of time which are identical in their ratios, just as it has made it possible for us to create sine waves in exact proportions. Drums can be carefully crafted to fit into music well. I've often used a combination of a repeated sequenced drum sample and a real drum hit (for variation on the original), but not strictly different hits each time because each hit has significantly different tonal (harmonic) qualitities.
CHANGING HARMONICS
I have also found that sometimes instruments whose harmonic content changes over time are less offensive to the ear. A good example of this might be something like a pulse wave, whose pulse width is being modulated by a triangle wave.
SUSTAINED SAMPLES OF THE WORLD
I have also noticed that single decaying chords of an instrument, or the repetitious sound of a sampler which plays a quickly repeating selection of sound has much potential for beauty, even if the sounds contain a high amount of dissonance. This seems to be a contradiction to my comparison of quick passages versus sustained passages, but perhaps it is not the same because the attack of the instrument is missing. Our world is full of pleasant sounds and it is my intention to record these and work with them musically on a future record.
MASKING
Another strategy which is perhaps obvious, is masking dissonant harmonics by keeping their volumes very low. A level of misdirection is achieved by imposing dominant more perfect sounds in the recording.
PSYCHOLOGICAL PRINCIPLES
The thing that keeps music vital, which I think might apply to any art form, is change, creation, and modification. As consumers of art, we seem to have an unending appetite for things that are new. Newness excites us and keeps us interested in feelings and experiences to come, while we also celebrate the past.
TIME, OBSESSION AND PERSPECTIVE
In music, as in other art forms, time is an important psychological quantity. Whenever we leave a project and come back at a later point in time, our perception of it changes. We are more objective because the lens of our focus has backed away from whatever we were studying before. Perhaps some short term memory gets erased. Whatever the case is, it is a reliable fact that it feels different.
I found that this worked well for my problem with harmonics. I found that it often took some time for my focus to shift from the good harmonics of a recording to the bad. But, repeated listening caused their flaws to become more and more apparent in my mind. They disturbed me so that I could not focus on anything but the bad, no matter how small their volumes. This is how I know about the relativity of our perception of good things and bad. This, of course, extends to our perceptions of pleasure in pain in life. If we can use this principle to our advantage, and make the pleasure we are given in life (no matter how small) seem to be outweighing the pain, then that is certainly an important skill. When I did recordings of natural instruments in 2009, I had to train myself not to examine the sounds too much. I set limits on how much I would try to improve the sound. I accepted that these recordings would be flawed and I completed them with pleasure and ease.
As I mentioned, it is possible for a person to fixate on the smallest details and expand them into unreasonable proportions. I found that as an artist, the key to sucess is understanding another form of relativity. By that I mean, most people who hear recordings will be hearing them with fresh ears. The sound is so foreign to them at the beginning that they are free to enjoy it. This is why for years I thought that radio music was harmonically superior to mine. But, it was only because I had no reason to pay such close attention to them.
It's always a little funny to me to see people go crazy over what guitars, amps, electronics and strings they use. An outsider can clearly see this person has fallen victim to what I would call a magnifying glass view of things (as an obsessive detail oriented person I have been often a victim of this myself). This is how I often visualize the psychological effect I described, which is as people become closer and closer to something their obsession and fixation on detail becomes greater and greater. It helps to know the principle of diminishing returns. This principle says basically that the rewards for any human effort, go down as the effort or time increases.
The human ear can focus in on a particular frequency band much like the eye has a central focal point. We can still hear the entire frequency spectrum with our "peripheral" hearing. I believe though, that unlike vision our focus becomes sharper over time and we tend to block out peripheral and focus on a narrow band.
[picture of focus vs peripheral hearing]
When listening to music, our perception of it can change over time. I have emphasized what I think are the merits of sinusoidal perfect music, but negative perceptions may occur, even if the music doesn't contain dissonant harmonics. I will have to experiment more with this.
GHOSTS
In the past when I have been working on some mathematically perfect music that I am certain is engineered correctly, I sometimes thought I heard harmonics or suggestions of harmonics that aren't there. At first I observed that this was because I used the equal tempered scale, and so the sine waves were not combining exactly right. With computer technology, I was easily able to make music in the correct mathematical relationships. Still, at times I thought I heard the ghosts. I believe these may be a natural phenomenon first described by Hermann Helmholtz where two summed sine waves created a third frequency which could be clearly heard separate from the other two. I am not sure about what I heard. It could be based on the interaction of two sine waves, or it could be a physiological phenomenon, or perhaps just imagination. I wondered if the ear accidentally creates harmonics that are not there, or if certain sine wave combinations psychologically suggest other frequencies, or perhaps I am so used to real world instruments creating the dissonant harmonics, that I heard them from these memories. It is interesting, but very subtle.
LIVE PERFORMANCES
In my experience, I have found that people are much less critical of live performances than recordings. In a way this is ironic because great care is taken to make studio recordings as close to perfect as possible and live performances are often riddled with mistakes in timing and many other things. The reason why this occurs, though, is because live performances are a one time occurance. Everything is new and the stimulation of other senses lessens a persons critical ability. Every stroke of instrument is different from what they've heard before. There is little short term memory in operation. Even if the listener heard recordings of the material before, it will not sound exactly the same live as it did at any time before. Actually this is often the performance's appeal. In studio recordings, we hear the same frequencies over and over again. Our memory becomes involved and we can quickly memorize things we dislike.
I've always enjoyed playing live much more than I've enjoyed listening to the recordings that I've made. Before I became involved with recording, sound was closely connected to a palpable and visual instrument. My interactions with it produced notes with different harmonics each time. In a live setting music is dynamic. We are influenced and misdirected by our other senses. This is not so in recorded music, except when it is accompanied by videos or something else that is distracting.
CHANGES IN PUBLISHING
It has always been my tendency not to group my recordings into music albums. The initial reason is that I was dissatisfied with the quality of my recordings enough that I didn't see the point of declaring them an album, and certainly did not want to declare them a finished product. However, there were times I had the dream and intention of grouping songs into albums. In January of 2009 after I learned a lot about psychology and recording, I was determined to finish an album. I did about 10 recordings and I called this "The Romance of the Strings." I called it The Romance of the Strings because of my love of the sound of stringed instruments, and my struggle in youth to accept their imperfections. Another meaning is that I have been heavily influenced by the romantic piano music I listened to and played as a teenager. Yet another is that much of my music contains romantic themes. However, although I have considered grouping at different times, I have usually abandoned the idea afterwards and I've actually created very few physical discs of my music.
I believe that the internet will make the entire concept of the music album obsolete. In the past songs were released in a group as a matter of practicality. It probably wasn't practical to manufacture and distribute only a couple songs on a physical disc, tape or record. However, those old models of distribution are dying and there is no reason to group songs unless the artist chooses to do it. I imagine some artists might still wish to group songs based on various criteria. An artist might wish to group songs based on date the song was written, song style, but in the future such organization will really be intellectual only. Since all songs will be distributed digitally, the grouping is an intellectual exercise only, and I suppose could often be done at any time. There are many things I find particularly interesting and exciting about the new technology. Recordings can be updated and improved and redistributed by artists at any time. Content can be accessed as soon as it is completed by the artist. I've been leaning toward utilizing these methods of distribution. Also, I feel that songs have some degree of timelessness to them and so, the performing and recording of them should be an ongoing process. This also has benefits to the quality of recordings, artists can improve their recordings over time and get ever closer to where they believe the song should be. On the other hand, perhaps some will argue that it is better to have a recording and a song and an album represent who an artist was at a particular point in time. SONGWRITING
Songs are ideas. They can be played and recorded, but what they really are, is mental objects. They exist in the minds of the creator and listener. The elements of a song can, of course, be expressed on paper and today, in recordings. Songs have elements of perfection and imperfection.
Songs are perfect in that they are a perfect expressions of what a person wishes to convey at a particular time. In the previous section I explained how mathematics gives us ratios with which to create music. But, the utilization of these ratios is entirely up to us. The chords we choose to use in our songs are mathematical in nature. In sequences, we find that the mind enjoys symmetrical time lengths and rhythms. In the past, the perfection of rhythm was limited to a performer's sense of time. Today, we can use technology and machines to alter or keep perfect time. Thus, machines have solved one of the sources of imperfection in performed and recorded music.
CONCLUSIONS
My journey in music has been a long one, driven by passion, and the idealism and admiration of my youth. I was drawn in by the emotions and power of music. I imagined that the art of sound recording was analogous to the visual arts, and as in art, material would flow from my mind in a limitless fashion. In some ways it did, and in others it did not. When I reflect on my original intentions, I realize that for a time, the experience of making music did not turn out to be exactly how I imagined it would be. I imagined that making music and sound recordings would be easy, and would be infinitely pleasing to me, and a legacy of what I had done. The reality was that like many endeavors in life, as time went on I found that getting to that point in music recording was much, much more difficult and complex than I ever expected. A simple proficiency in the arts of songwriting, musicianship and recording music has taken eight or more years for me, with a few life interruptions in between, of course. The art of songwriting seemed at first very difficult, but I improved my ability to write songs to a surprising degree. Now that I believe I understand many important principles of music and psychology I am much more at ease about things. I can accept music's true nature and take from it what I can.
My conclusions thus far about music is that it is operating on an infinite number of levels simultaneously. I also found that in practice, it is unfortunately very difficult for a person to enjoy and feel secure in the love of their own natural recordings. I particularly was troubled because some of the time that I listened to them, they sounded great, and some of the time they did not. I wonder now if the visual arts are actually more pure than sound recording. In the visual arts one uses all the colors of the spectrum to cover the blank canvas. These colors are logical and pure, whereas the sound spectrum is chaotic and can often only be partially organized. Natural instruments, on the other hand, inherently contain a profound amount of flaws. But, it is in the partial organization of the frequency spectrum that we find pleasure. On some levels, such as in the timing, the expression of an idea, in the documentation of some part of history, a traditional recording may be quite perfect, but in others such as harmonics, and vocal performance, it can not be. However, as I hope I've shown, real world instrument recordings are not completely lost because of imperfections. Imperfect recordings have much to offer. When I created The Romance of The Strings, I accepted that my recordings would be flawed in many respects, but I realized that they still offer a great deal. It is sometimes possible to ignore the technicalities of a recording and just focus on the perfect beauty of the ideas being conveyed. People do this every day when they listen to the radio. I do this myself when I perform or listen to live music. None of us will escape difficulties and painful feelings in life.
I wonder if in the future we can improve real world instrument recordings music by making them less fixed than they are now. Perhaps our recordings will be changed and modified in some random way by a music player, in order to keep them new and interesting to the listener. But even as I imagine this, I realize that this phenomenon already exists in way. Every amplifier, speaker and room has a different frequency response. In fact, the songs themselves sound different every time we listen based on what mental and physical state we are in at the time. Also, musicians are constantly creating new recordings, and this keeps music dynamic and interesting to listeners.
But, I wondered if it was possible to create music that dependably evokes a positive response within us. So far I am convinced this is not just an idealistic fantasy. I have only just begun exploring the so-called "perfect" instrumental music I described, but I have found that it puts me at ease much more than my typical recordings. I have pointed out many directions through which a more perfect expression of music is possible, and grey areas through which a more perfect natural music may be achieved.
In the distant future, perhaps questions of our psychological appreciation for music will be unnecessary. Perhaps the living beings of the future will be engineered to feel no pain, and they will have their own kind of mathematical music, which is nothing like our natural music today. Wouldn't that be interesting?
As I said previously in my journal, we humans take pride in our ability to struggle, endure difficulties, and seek answers to our questions. I continued on this path out of curiosity among other reasons. I have enjoyed many things about making music. Some of my favorite times have been performing and encountering interesting people and places. I have enjoyed songwriting. Years ago I would have to work for many many days to create a single song, but today I can write them very very quickly. Thus, many parts of my dream have been fulfilled. It is also enjoyable to me to hear that other people enjoy the music I have written and performed.
I have been ambitious and perfectionistic in my approach to understanding music, but that is not really surprising. Perfectionism seems to be present in all of us due to our evolution. It is precisely our perfectionism that has propelled us to higher and higher levels. I have been very happy to be able to report the things I have found. Discovering some truths about music through experimentation and learning from others, and describing them in writing has been quite fulfilling.